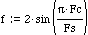1.8 KiB
https://www.earlevel.com/main/2003/03/02/the-digital-state-variable-filter/
The frequency control coefficient, f, is defined as
where Fs is the sample rate and Fc is the filter’s corner frequency you want to set. The q coefficient is defined as
where Q normally ranges from 0.5 to inifinity (where the filter oscillates).
The main drawback of the digital state variable is that it becomes unstable at higher frequencies. It depends on the Q setting, but basically the upper bound of stability is about where f reaches 1, which is at one-sixth of the sample rate (8 kHz at 48 kHz). The only way around this is to oversample. A simple way to double the filter’s sample rate (and thereby double the filter’s frequency range) is to run the filter twice with the same input sample, and discard one output sample.
example with double-sampling
input = input buffer;
output = output buffer;
fs = sampling frequency;
fc = cutoff frequency normally something like:
440.0*pow(2.0, (midi_note - 69.0)/12.0);
res = resonance 0 to 1;
drive = internal distortion 0 to 0.1
freq = 2.0*sin(PI*MIN(0.25, fc/(fs*2))); // the fs*2 is because it's double sampled
damp = MIN(2.0*(1.0 - pow(res, 0.25)), MIN(2.0, 2.0/freq - freq*0.5));
notch = notch output
low = low pass output
high = high pass output
band = band pass output
peak = peaking output = low - high
--
double sampled svf loop:
for (i=0; i<numSamples; i++)
{
in = input[i];
notch = in - damp*band;
low = low + freq*band;
high = notch - low;
band = freq*high + band - drive*band*band*band;
out = 0.5*(notch or low or high or band or peak);
notch = in - damp*band;
low = low + freq*band;
high = notch - low;
band = freq*high + band - drive*band*band*band;
out += 0.5*(same out as above);
output[i] = out;
}